World record slide rule, the Eximius Diu 6

Here is my attempt at a large, practical, and accurate slide rule...

2012. 175 m (574 ft) long scale. The Eximius Diu 6, by Dave Hoyer. Spiral slide rule, 750 mm (29.5") diameter, 135 spiral turns, scale length 175 m (574 ft), equivalent linear length 318 m (1043 ft). Relatively easy to operate, with 6 digits accuracy over the whole range.

Previous world records

Ref. The Slide Rule Guy

1973-74. 20 feet long, 110 pounds (6.1 m, 50 kg). Constructed by Ralph Nyberg and members of the Mathematics Club of Roanoke-Benson High School, Illinois. Guiness Book of World Records, 1976, Sterling Publishing Co, New York, NY USA.
1978. 59 feet 1 1/4 inches (17.9 m) in length designed by Ralph J. Snelson and R. Clayton Brough and built by students at Springville Junior High School, Springville, Utah. Guiness Book of World Records, 1978, Sterling Publishing Co, New York, NY USA.
1979. 320 feet 11.1 inches (97.4 m) in length completed in March, 1979, by students of Alvirne High School, Hudson, New Hampshire. Guiness Book of World Records, 1980, Sterling Publishing Co, New York, NY USA.
1983. 323 feet 9.5 inches (98.3 m) in length completed on Nov 11, 1979 by Greg Maggs and Robert Kolstad at the University of Illinois College of Law Building in Champaign, Ill. Guiness Book of World Records, 1983, Sterling Publishing Co, New York, NY USA.
2001. 350 feet 6.6 inches (106.4 m). The Texas Magnum, by Skip Solberg, was demonstrated on February 28, 2001 in the Lockheed-Martin Aircraft Assembly Facility at Air Force Plant 4 in Fort Worth, Texas. It weighs over 300 pounds (136 kg) when assembled and takes 3 people to operate.

Make your own Eximius Diu 6

Scroll down to download a printable image of my Eximius Diu 6... Here

Accuray and precision of slide rules

Some thoughts on the meaning of the terms accuracy and precision, and how to determine the number of significant digits of a slide rule... Here

Eximius Diu 6

Spiral slide rules are more compact than linear and cylindrical ones for very long scales. They have the added advantage that the inner turns of the slide rule are shorter than the outer turns. If we arrange the scale so that the numbers increase from inner to outer, and the inner spiral turn is one tenth the diameter of the outer, then the accuracy will be the same at the beginning and end of the spiral. The accuracy is about the same (slightly better) within the interior of the spiral.

I wrote a computer program to generate an image of the spiral, add markers and text at the correct logarithmic locations along the spiral, and add some colors etc. Ignoring the irony that it took a computer to generate the slide rule (though it's quite possible to generate the slide rule manually as it would have been done in the old days), the result is a usable slide rule that is accurate to 6 decimal places across its whole range. You need to be very careful to get that last digit of accuracy.

The slide rule was printed at 600 dpi on A0 paper, then trimmed and laminated. The spiral diameter is 750 mm (29.5"), with 135 spiral turns giving a scale length of 175 m (574 ft). Due to the nature of spiral slide rule scales, this is equivalent to a linear slide rule of length 318 m (1043 ft). In other words, a linear or straight slide rule would need to be 318 m long in order to have the same 6 digits minimum accuracy at all points: Linear slide rules are 10 times more accurate at the low end near 1 than at the top end near 10, whereas a spiral slide rule can compromise by making the accuracy more constant from end to end.

For a more detailed explanation of slide rule accuracy see... Slide rule accuracy

There is also a circular slide rule around the outside of the spiral. Its diameter is 760 mm, making a length of about 2.4 m. This circular slide rule is used for a quick lower-precision estimate of the answer (4 digits precision).

Two additional sheets of clear plastic film were cut to the diameter of the spiral, scored with a pin to make a very thin marker line from the centre to the edge, and pinned over the laminated printout to become the equivalent of the two cursors.

Using the Eximius Diu slide rule

Spiral slide rules need two cursors. My version 1 used two transparent layers over the whole slide rule, with a pin for the layers to rotate about (see EximiusDiu6 v1). Each layer had a cursor line etched from the centre to the outer edge. This worked quite well, but was a little fragile and the two layers weren't as transparent as I'd hoped, and it was a little clunky to use. So for this version I used parts from a spare 8" Gilson slide rule similar to my Gilson Atlas spiral slide rule (the parts were carefully removed and can easily be replaced back into the original Gilson).

So now my Eximius Diu (version 2) has a high-resolution image printed on good quality paper and stuck onto a circular base cut to size from acrylic sheet. Then I had two cursors cut from thin (1 mm) polycarbonate and assembled into the Gilson cursor mechanism, which was then mounted into the centre of the slide rule.

The Eximius Diu 6 (version 2.1) slide rule. The spiral is 750mm diameter (about 30"), printed on paper, laminated, and stuck onto a circular piece of acrylic (perspex). You can see the Gilson cursor mechanism and the two cursors arranged in the "4 o'clock" position. The cursor mechanism is very clever actually - moving the first cursor will drag the second cursor along with it, but moving the second cursor leaves the first one where it was.

The image shows a size comparison between the Eximius Diu 6 and the Gilson Atlas spiral slide rule (lower right). To left of the Gilson are the Fowlers Long Scale Calulator and Fowlers Jubilee Magnum Extra Long Scale. The Gilson is about 200 mm (8") diameter, and the Eximius Diu about 770 mm diameter.

Click the image for a larger view.

Close-up view of the cursor mechanism.

The Eximius Diu has a lot of very small numbers and it's not always easy to find the one you're looking for, so I've used colours to help as much as possible. I adapted the colour scheme of the Gilson, which uses alternating yellow and white backgrounds for the decades within the slide rule (1-2, 2-3, etc). I used the same alternating bands, but then also alternated light and dark within each band. I added colored circles around the big numbers - red for 1, 2, ..9, and light blue for 11, 12, .. 98, 99 etc. Major tick marks are coloured red, black for minor ticks.

Doing a calculation - let's try 1.23456 * 4.56789. The correct answer to 6 decimal places is 5.63933. First we use the outer circular slide rule to get an approximate result (we need this for later).

Align Cursor A so that its etched line goes through 1 on the outer circular slide rule, as shown in the photo at left.

Keeping Cursor A fixed over 1, rotate Cursor B to pass through the first multiplicand (1.234 is about the closest we can manage on the circular rule).

Cursors A and B can be rotated together around the slide rule without changing their position relative to each other. If you rotate Cursor A, Cursor B will follow. We need to preserve the angle between the two cursors.

Rotate Cursors A and B together until Cursor A's line goes through the second multiplicand (approx 4.568)

Now Cursor B's line will lie on the solution. The image shows both cursors.

Zoomed in on Cursor B. We can write down the approximate solution as 5.64 or maybe 5.639

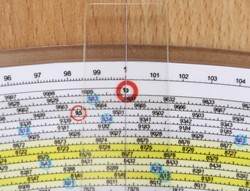
Now we know the approximate answer, so we can go ahead and do the calculation at 6 digits precision using the spiral slide rule. It's a similar procedure. First align Cursor A so that its etched line goes through 10 (it will also go through 1 and the centre).

Keeping Cursor A fixed over 10, rotate Cursor B to pass through the first multiplicand (1.23456). The adjacent numbers 1.234 and 1.235 are printed on the slide rule, with 10 sub-divisions marked with ticks, so you can easily count the ticks to get 1.2345, and and then estimate 60% of the way between 1.2345 and 1.2346 to get 1.23456. This needs to be done very carefully.

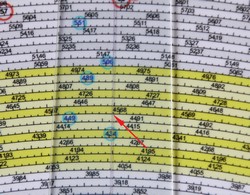Next rotate Cursors A and B together until Cursor A's line goes through the second multiplicand (4.56789)

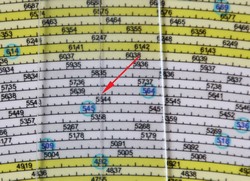Now Cursor B's line will pass through the solution, which will lie on one of the 135 turns of the spiral. We just need to find which turn of the spiral is the correct one. This is why we needed to know the approximate result first. Search the spiral turns to locate the one closest to 5.64, which is the approximate result we obtained earlier from the outer circular slide rule. Then we can (very carefully) read off the result to be about 5.63932 (see the red arrow). The correct answer is 5.63933, so we were pretty close here, and within the 6 decimal places accuracy.

There's the final step that should be done as a sanity check. Rotate Cursors A and B together until it has gone full circle and A is back where it started at 1. If the cursors remained correctly locked together then Cursor B should again be pointing at the first multiplicand 1.23456

Some low res images

The slide rule is a bit big to show here at its full resolution (at 600 dpi and 18,000 x 18,000 pixels the png file size is 28MB).

Meanwhile here are a few lower resolution images, starting with the whole slide rule, diameter 750 mm. Click on the image to see it at about actual size, but with the resolution reduced to 120 dpi.

About actual size, resolution reduced to 120 dpi. Use the scroll bars to scroll the image...

Zoomed in the area around 10..

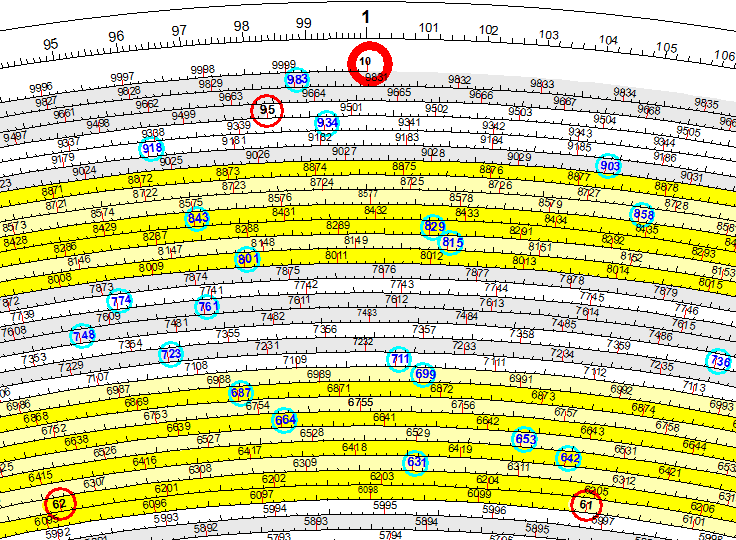
Zoomed in the area around 1..

Zoomed in the centre area..

Make your own Eximius Diu 6..

Download a high resolution (600 dpi) PDF file that you can print and laminate. Print it on A0 or similar size paper, sized so that the diameter of outer circle around the spiral is 774 mm (about 30.5"). Optionally - laminate it. Then make the two cursors, you might have to use some ingenuity here ;-) I showed how to use two transparent layers in version 1, and how to use a Gilson mechanism in this version 2. Just make sure each cursor has a thin line etched underneath, and that the lines would extend back to the exact centre of the slide rule. You also need to be able to lock the two cursors so that you can rotate them together. You might also consider using a CD/DVD case similar to that shown by Ying Hum here. Let me know if you find a better way of doing the cursor.

Downloads..

Please note these images and pdf's are copyright. They can however be downloaded and printed freely for any use. Please give acknowledgement if distributing them. If you make one of these, I'd be interested to know - just drop a note in the guest book. Dave Hoyer, Aug 2013.

Eximius Diu 6, pdf (22 MB). This is the file I had printed at my local commercial printer, they seem to prefer pdf files. Print it on A0 paper, outer circle should be 774 mm diameter.
6 x A3 images, png (34 MB). Zip file contains 6 PNG images to print on A3 paper at 600 dpi resolution. There is a small overlap so that you can align the images when sticking them together.
12 x A4 images, png (32 MB). Zip file contains 12 PNG images with overlap, to print on A4 paper at 600 dpi resolution.